
KLANGPILOT - a software environement for
control and composing of synthetic sounds
Johannes Kretz
ABSTRACT:
KLANGPILOT is a software environment for describing and generating (mainly) synthetic sounds.
The KLANGPILOT language, an extension of the computer language CommonLisp, is designed in a way rather close to how traditionally educated composers might think of or describe musical sounds, that is: an extension to the usual paradigm of notes organized in scores realized by instruments. But: a lot of additional features can be added to this "notes" and "instruments" allowing an extensive control on each partial at each moment. The main approach is a perceptive one: the creation of sounds by concentrating on the desired results rather than their causes. Therefore, especially those methods of synthesis were implemented in KLANGPILOT, where FFT (Fast Fourier Transform) analysis allows to find the required parameters of synthesis for almost any given sound. Also, several methods of synthesis can be combined an controlled in such an "instrument" simultaniously, and transitions between the instruments (morphing, hybrids) are easily defined. The work with KLANGPILOT can take advantage of the full possibilities of CommonLisp at any moment, wich means that instruments or scores can also be generated by LISP functions, leading to a flexible integration of the techniques of computer aided composition.
1. Introduction
The developement of KLANGPILOT started 1992, during my studies at IRCAM, under the impression and direct and indirect influence of the corresponding work by Marco Stroppa, Magnus Lindberg, Francis Courtot, Jan Vandenheede, Steven McAdams and the Patchwork-environement (IRCAM, J. Duthen, M.Laurson and C. Rueda). The first prototype was finished in 1993 and used to realize several compositions until 1996 (see section 5). In 1997, supported by a generous grant of the austrian gouvernement (Bundeskanzleramt, Sektion Kunst) and some financial aid provided by the town of Vienna, a complete rewrite of the software-environement with a lot of improvements and new features was done.
1.1 Why synthesis ? Flexible navigation between timbres
One of the main ideas in developing KLANGPILOT was the wish to navigate freely and smoothely in the space of timbre. This seemed to be very difficult using writing techniques for acoustic instruments and still problematic if only applying sound treatment on recorded sounds. So, from the beginning, the basic idea was to realize synthetic sounds of high quality, as close as possible to recorded sounds of acoustic instruments or other sources, and then to interpolate the synthesis parameters (maybe not only in a linear way) to obtain transitions between those synthetic "instruments".

Fig. 1: Graphical analogon of a timbral transition
1.2 Again: Why synthesis ? The idea of timbre-harmony
The second wish, which is again almost impossible if not using computer generated sounds, is the idea of controlling and composing partials in a subtle way, comparable to the way of composing chords in polyphonic music. The vision of a music, where chords are melted or fused into timbres, and timbres are controlled by the composer like chords, leads to the border between harmony and timbre, an exciting unexplored area for new music. Already Arnold Schönberg described this vision at the end of his book on harmony ("Harmonielehre", 1911, and probably tried to realize it in the third of his orchestra pieces op.16.) But today we finally seem to have the means to master this new approach of music.

Fig. 2: First chord of A.Schönberg op.16/3 "Farben" ("Colours")
1.3 Which methods of synthesis to use ?
Because of the perceptual approach, the synthesis methods implemented in KLANGPILOT are those, where synthesis parameters can be easily derived from the Fast Fourier Analysis (FFT) of any given sound. Currently, the following methods are supported:
(which is of course the most general method and can be regarded as a sort of inverse Fourier transform. About 80% of the frequently used KLANGPILOT instruments are based on this method. Especially interpolation between sounds is easy and perceptually convincing.)
(that is: filtered white noise, especially useful for noisy sounds, "wind instruments", blowing noises, but also short unpitched attacks. This method can be regarded as a complement to additive synthesis, to obtain sounds, that are difficult to get by adding sinewaves.)
(very powerful for simulation of human voice, especially vowels.)
(not much developed at the moment. Can be used for plucked strings or drum like sounds. At the moment it is not fully integreated in the environement.)
(can be used for algorithmic mixing of an almost arbitrary number of sound files. Also turned out to be interesting to generate synthetic sounds based on chords, then apply corresponding filterings to soundfiles using the same parameters and to mix the results.)
Frequency modulation and physical modelling are not implemented, as they do not have such direct relation between synthesis parameters and perceptual result.
2. Control of sound synthesis
The software-environement, programmed in LISP does not generate sound itself, but it creates huge scores for the Csound audio processing system (Barry Vercoe, Media Lab, M.I.T.), which are then compiled into soundfiles by Csound. The Csound orchestra of KLANGPILOT consists of six instruments corresponding to the synthesis methods mentioned above. In this sense, the LISP part of KLANGPILOT can be regarded rather as a software for controlling sound synthesis than for generating sounds. But this sophisticated control interface between the user and Csound environement allows to work with sounds in a merely human oriented way without having to worry about hundreds of more or less abstract sound synthesis parameters during the process of composition.
2.1 Overview
One of the typical ways of using KLANGPILOT is to start with some recorded sound material, and to extract synthesis parameters from it. (It is also possible to derive these parameters from other sources like chords, which will be discussed later, see section 2.5) Currently I use AudioSculpt (IRCAM) as interface for the FFT analysis of sounds. This measured data have to be interpreted and abstracted into KLANGPILOT instruments. At the moment, there is no automatic way to do that (except of some very experimental LISP functions.) But the decision about the perceptually relevant properties of a sound often is an aesthetic choice, anyway. These "instruments" or sound prototypes are stored in a data base and can then be called from a KLANGPILOT score. Scores can either be typed or generated (for example by some method of computer aided composition.) The kernel of the LISP part of KLANGPILOT then compiles the information of instruments and score into a Csound score, which is then compiled (in a second step) into a soundfile.
Fig. 3: Overview on the work with the KLANGPILOT environement
2.2 Creating instruments
The translation of the analysis data into a KLANGPILOT instrument has of course to take into account the stucture of the particular Csound instruments for each synthesis method. To give an example: For additive synthesis I use the following:

Fig. 4: Diagram of the Csound instrument used for additive synthesis
The following (fig. 6) KLANGPILOT instrument, derived from the sound of a bass clarinet (and therefore named bass-clar1), uses two methods of synthesis, additive (addsyn) for the body of the sound and subtractive (filtered white noise, fwn) for the blowing noise at the beginning. For each synthesis method, the corresponding parameters are marked by a keyword, allowing to identify the kind of data, and subsequently the data themselves. The time-offsets in this example are set to zero, (but a list of different values for each partial would allow here a kind of spectral arpeggio.) The durations (durs) of all partials of the additive synthesis module are set to 100, meaning 100% of the duration of each note calling this instrument, but the durations of the fwn module are set to (a 1.2), meaning that the blowing noise occurs only at the first 1.2 seconds absolutely, that is, independently from the length of the note. Other parameters are:
ampls: general amplitudes of the partials in dB.
ampl-kind: The amplitude envelopes can be 'LIN (linear) or 'EXP (exponential)
ampl-envs: Amplitude envelopes are descibed as pairs of coordinates. As both axes (duration and amplitude) are rescaled, the coordinates just go from 0 to 100. (see fig. 5). If some points of the envelope should not be rescaled according to the duration of the "note", one can use points in the form (a 2 80), meaning that 80% of amplitude will be reached after 2 seconds (absolute time) independently of the duration of the note. (The note should be longer than this 2 seconds, of course.) This "absolute points" in time are especially usefull to create attacks of sounds, that are usually independent in their duration from note length. If the number of envelopes is smaller then the number of partials, then additional envelopes are generated by KLANGPILOT by interpolation of the given shapes.
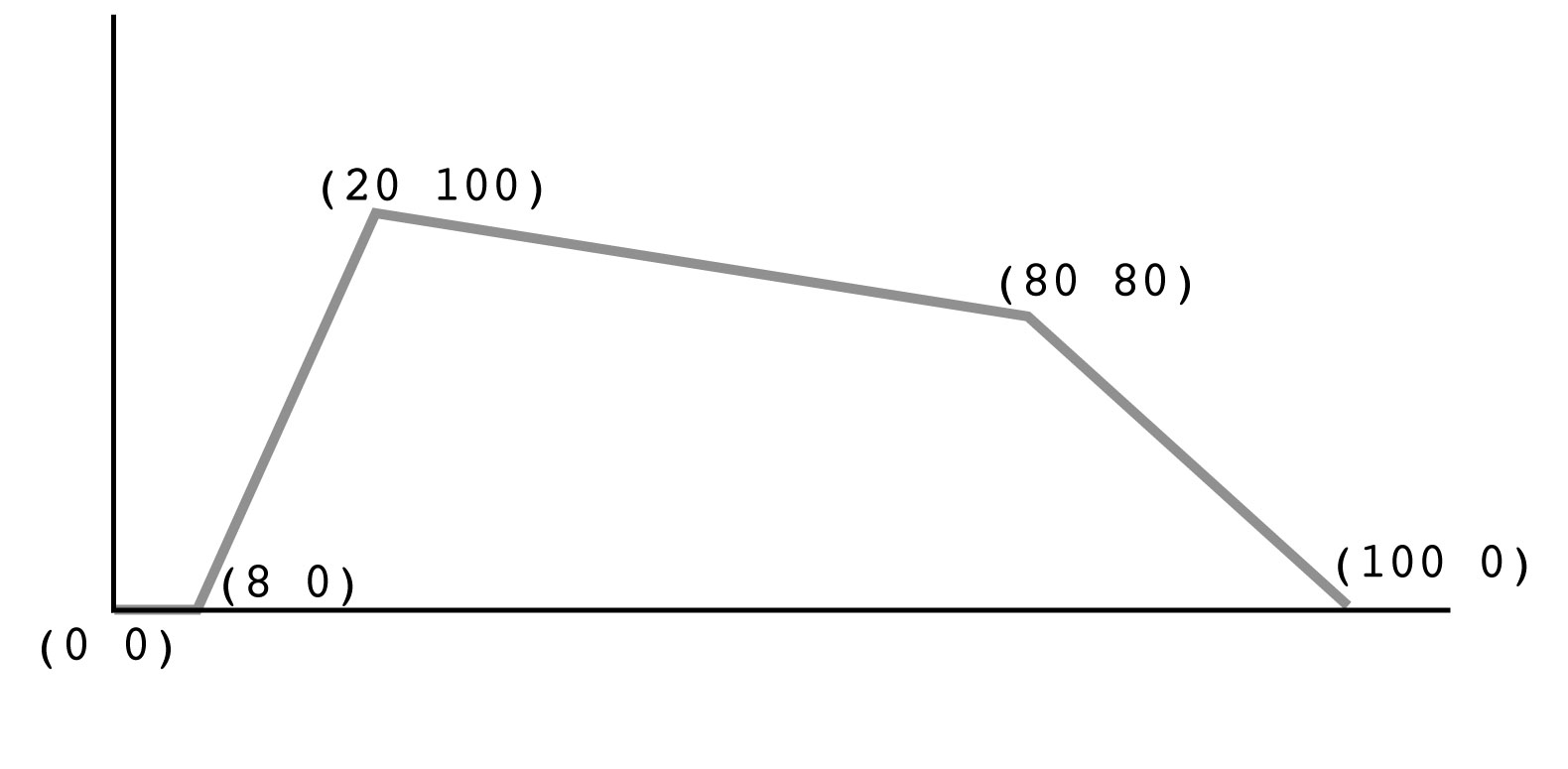
Fig. 5: Amplitude envelope
freqs: Frequencies of partials in Hertz, could be modified by linear or exponential evelopes (freqs-envs), describing the deviation from the original frequenciy (in semitones). This envelopes can contain points of absolute time in the same way as ampltude envelopes.
A lot of attention was given to all kind of little fluctuations of partials, that give inner live to sounds and let them appear less sterile or synthetic in a bad sense. All this fluctuations are controled by two envelopes each: One for the strength (amplitude) of the modulation, one for the speed (frequency):
Amplitude modulation (periodic tremolo): am-a-envs, am-f-envs
Frequency modulation (periodic vibrato): fm-a-envs, fm-f-envs
Amplitude jitter (random amplitude fluctuation of partials): aj-a-envs, aj-f-envs
Frequency jitter (random frequency fluctuation of partials): fj-a-envs, fj-f-envs
The fwn module uses lists of bandwiths (bws) and bandwith-envelopes (bw-envs) for controlling its bandpass filters. What can also be seen in the example (fig. 6) is, that at any place LISP functions or KLANGPILOT functions can be called to define the instrument in a more formalized way: (a-sn 20 2000 87) for example means an arithmetic series from 20 to 2000 in 87 steps.
(setf bass-clar1
(mapcar 'eval '
('bass-clar1
'(methods addsyn
fwn )
(list
'(kind addsyn)
'(time-offsets 0)
'(durs 100)
'(ampls (80 54 81 58 73 58 66 48 64 58 63 62 69
64 60 ....))
'(ampl-kind LIN)
'(ampl-envs (((0 0)(8 0)(20 100.0) (80.0 80.0) (100.0
0.0)) ((0 0)(8 0)(30 40.0) (60.0 90.0) (100.0 0.0))))
'(freqs (262 527 794 1060 1319 1583 1848 2116 2380....
))
'(freq-kind LIN) '(am-a-envs (((0 50) (100 60))
((0 70) (100 60))))
'(am-f-envs (((0 10) (100 20)) ((0 15) (100 20))))
'(aj-a-envs (((0 80) (100 60)) ((0 60) (100 80))))
'(aj-f-envs (((0 .8) (100 .9))((0 .1) (100 .2)))))
(list '(kind
fwn)
'(time-offsets 0)
'(durs (a 1.2))
(list 'ampls (g+ -21 ' (80 54 81 58 73 58 66 48
64 58 62....))))
'(ampl-envs (((0.0 0.0) (50 100.0)(80 40.0)(100.0
0.0)) ((0.0 0.0) (5 100.0)(80 40.0)(100.0 0.0))))
'(ampl-kind LIN)
(list 'freqs (g* .9 '(262 527 794 1060 1319 1583
1848 .... )))
'(freq-kind LIN) (list 'bws (a-sn 20 2000 87))
'(bw-envs (((0 -40)(50 0) (100 -80))))))))
Fig. 6: Example of a KLANGPILOT instrument
2.3 The syntax of Klangpilot scores
The KLANGPILOT instruments can be seen as prototypes of sounds, that can then be called, modified, interpolated and even redefined from a score. Pitches and transitions of pitches (glissandos) can be specified in the precision of eights of tones, quartertones or semitones. In addition to the traditional parameters of notes (instrument, time, duration, pitch, amplitude), the properties of the instrument can be modified in many ways: the (amplitude) envelopes can be softened or sharpend by an attack modifier. The spectral flux (that is all kinds of modulation and jitter together) can be emphasized or reduced for each note. The brightness can be controlled by another envelope. The spectrum can be distorted by a inharmonicity factor. Note, that each of these timbral modifications concerns one of the general sound properties, that psychoacoustics shows to be the dimensions of sound: percussivity, brightness, spectral flux, harmonicity. Furthermore specifying a "vowel envelope" allows to modify the spectral shape of an instrument in another way: by calling vowels. (these have to be defined before as a list of an arbitrary number of formants, where each formant is described by its center frequency, attenuation in dB and bandwith in hertz) The vowels can vary in time again as an envelope, like
((0 aa) (20 ee)(40 ii)(60 oo)(80 uu)), where aa could for examole be defined as
(setf AA '((609 0 78) (1000 6.1 88) (2450 12 123) (2700 11 128) (3240 23.8 138)))
Finally, each definition of each parameter of the instrument can be replaced by a new definition only valid for a special note.
Figure 7: Example of a KLANGPILOT score
Futhermore, KLANGPILOT scores can also be represented in a algorithmic way, by LISP functions, evaluating into a score of the same syntax as above:
(klangpilot "KLANGPILOT2" "histrclu-many2"
(turn-matrix(COMPLETE-ALL-LISTS
(list
'(histring)
(curve 0 6.0 17 .95)
(m-l 3 17)
(midi-note (a-sn 60 72 17))
(curve-bp 80 90 17 '(100 0 100 50 100 60 80 30 70 20 60 10))
nil nil '<<<<<<<< nil nil nil ))))
Figure 8: Example of a KLANGPILOT score in algorithmic style
2.4 The problem of pitch independent shapes
One of the properties of acoustic instruments is, that their spectrum varies depending on the fundamental frequency not just by a simple transposition of each overtone keeping the same amplitude. Usually, certain formants of the resonating system are constant, emphasizing different partials differently in notes of different pitches. Therefore KLANGPILOT allows to specify a "pitch independent shape", a general spectral envelope, that controls the amplitudes of the partials dependently of their actual transposition.
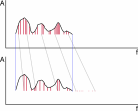
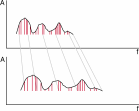
Figure 9a and 9b: Transposition of a spectrum with and without pitch independent shape
2.5 Generating instruments out of chords
As mentioned at the begining, one of the main interests of KLANGPILOT is exploring the border of harmony and timbre. To fuse chords into timbres, it turned out not to be sufficient just to play chords by sine tones. A couple of additional techniques had to be developed to make this more convincing:
First, the number of partial has to be increased. Chords might have a couple of notes (maybe between 3 and 12), but a series of partials for a synthetic instrument requires more (between 50 and thousands). The following kinds of "overtonizers" turned out to be usefull:
Boulezian pitch multiplication: A technique (which can be found as writing technique in Boulez' Marteau sans maitre) of multiplying chords by transposing them onto every pitch of the original chord.
Spectral mirror: On the basis of the highest note of the chord as an axis, each note gets a corresponding mirror note.
Random permutation of repeated frequency differences: This technique that allows to create an arbitrary number of partials still pointing on the principal frequencies of the chord, is based on the observation, that in the harmonic series, the frequency difference of two adjacent overtones is always equal to the fundamental frequency (for example: 100 200 300 400 ... Hertz). So, a natural extension of this approach would be to calculate the frequency differences, to generate a long list of this numbers in arbitrary permutations, and to sum up this differences starting with the frequency of the higest note. Actually the shape of the so generated "overtone series" looks quite close to the harmonic series, an it is still acoustically supporting the impression, that the few first frequencies are the principal ones.


Fig.10a and 10b: Boulezian pitch multiplication and spectral mirror

Fig. 11: Random permutation of repeated frequency differences
In addition to this techniques of getting more frequencies, the choice of the spectral envelope as well as all kinds of modulation and jitter may help to get a more fused image of the sound.
2.6 Developing formants out of chords
Another tool of KLANGPILOT allows the creation of formants on the basis of chords. In this way, a low sound can be coloured by a chord, wich leads again to interesting and ambigous results.
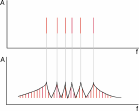
Fig. 12: Chords to formants
2.7 Hybrids, morphing
The creation of smooth transitions between two or more KLANGPILOT instruments was the most diffcult part of the developement. The main problem was, that a simple interpolation of frequencies did often not result in satisfying transitions. Especially when trying to interpolate quite different instruments having a different number of partials, the glissando effect as illustrated below caused the intermediate sounds to be too different from both original sounds. Finally the following method was developed: Partials that are closer than a certain threshold value (usually about 1 to 2.5 semitones) are interpolated by glissando, the other partials are blended by fading in or out. The same approach can be applied to interpolations between three and more instruments.
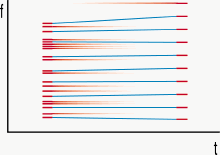
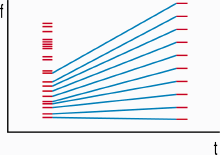
Fig 13a and 13b: Interpolation of freqencies with and without glissando artefacts.
A problem that could not be solved yet is the transition between instruments using different methods of synthesis. At the moment, only instrument moduls of corresponding methods are interpolated, and only additive and subtractive synthesis have been tested.
2.8 Clusters
To give sounds (especially those generated by additive synthesis) more body, another tool has been developed. The function make-cluster creates an arbitrary number of copies (or better "almost copies") of an KLANGPILOT instrument, where each partial of each copy has a certain individual deviation from the original. This micro clusters around each partial create sounds having more weight or body and can highly improve the quality of synthetic sounds.
Fig. 14: Sonogramm of a sound generated with additive synthesis, first without, then with the cluster option.
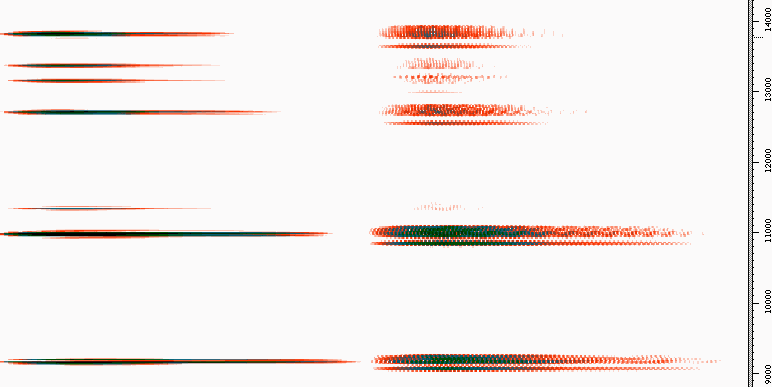
Fig. 15: Zoom in (Detail of fig. 14)
2.9 Data types
KLANGPILOT uses the following types of data:
Numbers and lists of numbers: representing frequencies, amplitudes, bandwiths, midi numbers ...
Symbols: are used mainly as keywords
Notation of pitches: '(c 4 n) = middle c
(a letter defines the pitch class, a number the octave and one of the following symbols the accidentals:
"+" = sharp, "-" = flat, "qtd" = quarter tone down, "qtu" = quarter tone up, "ned" = eight tone up, "neu" = eight tone down, "qeu" = quartertone plus eight tone up, "+eu" = semitone and eight tone up)
Envelopes: (see also section 2.2) Generally the spectral shape of a sound is represented as a three dimensional shape composed of several envelopes (break point functions), which are themselves composed by linear or exponential segments. These can be interpolated, even when having different numbers of segments, added, multiplied by other envelopes or numbers.
Fig. 16: spectral shape represented by a list of envelopes
3. Computer Aided Composition
As developing of a system for controling sound synthesis means formalizing at least a part of ones thinking about sound, timbres, transitions of sounds, phrasing, ... the step to enter the topics of computer aided composition (CAC) is not very far. KLANGPILOT contains currently two aspects of CAC:
3.1 "Harmony and counterpoint"
A quite developed engine exists for solving problems of chord generation: Starting (for example) from a given "mother chord" it can create a series of chords, that are all derived by transpositions and/or inversions from the "mother chord", where the number of common notes between two adjacent chords is maximized and certain progressions like jumps of all (or many) notes in the same direction are forbidden. Generally this engine can find chords derived from a first chord by some kinds of transformation (that have to be defined before), avoiding forbidden properties of the chords or progressions, and trying to optimize the result according to a given criterium. Especially when dealing with microtonal chords this can efficiently support the precompositorial process of a composition.
3.2 Linking parameters
Even closer to the problems of synthesis control is the appoach of linking musical parameters. Phrasing of melodies for example can be seen as setting the principal rythmic information in relation to the pitch information. A singer might need more time for realizing two notes in an interval of one and a half octaves, than two notes in the distance of a semitone. Rules like a correlation between intervallic and temporal distanceof two notes result in quite convincing phrasing. In the same way, timbre my vary according to the pitch range. Quite interesting results were obtained by splitting the pitch range of a melody into 4 or more regions, where the centers of the regions are associated with completely different instruments and the intermediate pitches are realized by timbral hybrids between these instruments. Human perception seems to be particularily sensitive to such relations between parameters like pitch and timbre, or pitch and rythm.
4. Implementation
The actual version of KLANGPILOT currently runs on Macintosh Common LISP (MCL 4.1) and Franz Allegro CommonLisp (for NeXT computers). Synthesis is done by Csound (M.I.T.). The LISP part uses quite a reduced set of basic LISP functions and should therefore be easy to port to any other implemetation of LISP. Csound, too is available for almost every computer platform. The only problem in porting the Csound part of KLANGPILOT from the NeXT to the Macintosh platform was the fact, that obviously the fof-module exists in different versions, having a different number and kind of inputs. At the moment, there exists no special graphical user interface for KLANGPILOT. To work with it, a certain knoledge of the LISP is recomended.
5. Works
The following works have been realized using KLANGPILOT:
"ELIA '98" UNERREICHBAR, VORÜBERGEHEND (1997/98)
Church opera. Text by Alfred Garcia Sobreira-Majer
"...BEWEGT ... VON KOMMENDEN ZEITEN ..." Music for 10 instruments and electronics (1996)
CompactDisc: "ÜBER-WEGS" MF 0098-01
"WO HAT SICH DEIN GOTT HINGEWANDT ?" (1994)
Cantata for mezzosoprano, choir, trumpet, piano, percussion and computer generated tape
"MENSCHENBAUWERKWEGE" (1996)
Cantata for soprano, choir, 2 oboes, trumpet, organ, string quartett and tape
DIE ENTDECKUNG DER LANGSAMKEIT I (1993)
for recorder, violoncello, percussion and computer generated tape
ETUDE for piano and tape (1994)
DIE ENTDECKUNG DER LANGSAMKEIT II (1993/94) for 4 trombones and computer generated tape
CD: Triton Trombone Quartett - BIS Records Schweden BIS-CD-694
DIE ENTDECKUNG DER LANGSAMKEIT III (1994) for 4 trombones and computer generated tape
SYMBIOSE (1997/98) for akkordeon and live electronics
DYNAMISCHE GEWÄCHSE (1999) for flute, clarinet, violin, violoncello, keyboard and electronics
Abbreviations:
FOF: formes d’ondes formantiques (fof, formantic synthesis)
FFT : Fast Fourier Transform
IRCAM: Institute de Recherche et Coordination Acoustique / Musique
M.I.T.: Massachusetts Institute of Technology